The Beauty of Reinforcement Learning (4) - World Model & Planning

How the concept of world model and planning brings new approaches to reinforcement learning, illustrated through AlphaGo & Dreamer agent.

A while ago, I played a game with LLM chatbots (ChatGPT / Gemini / DeepSeek). In the game, I asked them to pretend that the meanings of digit 2 and 3 are swapped wherever it shows up in the conversation that follows (but it is okay to use the original meaning in the thinking). I would then ask them a question where using lots of 2s and 3s are needed, for example:

Explain to me the ABC conjecture with extensive examples and illustrations.

No matter how hard I asked the chatbots to think, their responses always contained some error, where the original meaning of 2 and 3 were used. Some of the chatbots were actually quite sophisticated. They thought for minutes; they wrote code to swap digits in their demonstrations. However, when the thinking was done, they went back to the “mindless autocomplete” mode, when they just didn’t care what they output anymore. That “mindless autocomplete” mode was where mistakes came from, because, in the lengthy final output, there was always something that they didn’t think through during the thinking phase.

I found this game relatively easy for me. In contrast with the chatbots, as I wrote, word by word, I had in my imagination what I was going to write next, and I had predicted what would happen if I wrote that down. I used my simulation to plan what I should do next, continuously throughout the course, and it allowed me to do better than those chatbots in this game.

World Model and Planning

Can we define simulation and planning more rigorously? In a reinforcement learning setting, an agent takes an action, changes the environment from one state to another, and gets some immediate reward (which can be zero). Simulation fulfills the role of the real environment, by predicting the next state of the environment and the immediate reward given the current state and the action the agent would take. The model that does such a prediction is also called the “world model”.

With the help of the world model, the agent can imagine future trajectories. Let’s say the agent is currently at state s_t, and it is considering taking action a_t. With the help of world model, it can

• Predict the next state s_t+1, and immediate reward r_t+1;

• Use the agent’s policy to select the action a_t+1;

• Predict the next state s_t+2, and immediate reward r_t+2;

• …

Utilizing this imagined trajectory for training or inference is called planning. RL systems that don’t involve a world model are called “model free reinforcement learning”, otherwise it is called “model based reinforcement learning”. Figure 1 below shows the high level differences between these two RL paradigms.

Figure 1. model free reinforcement learning (left) vs model based reinforcement learning(right). Notice that for model based RL, “direct RL” is still an option.

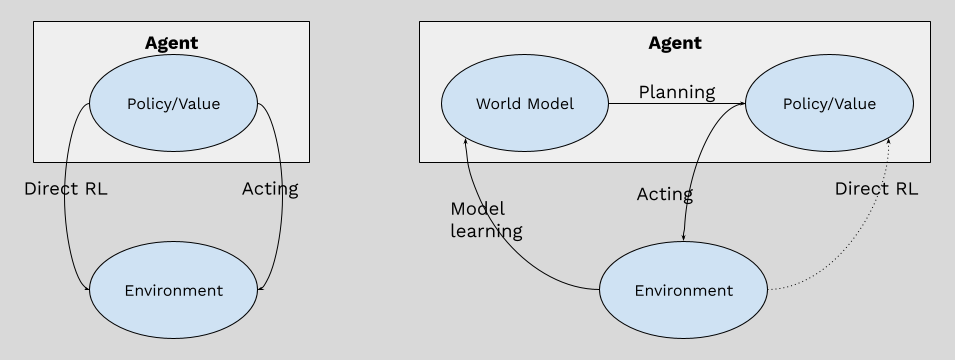
Planning can be used to improve the quality of an agent’s decision. The improved decision can be used at inference time, like what I did with the digit-meaning-swap game, or at training time to learn better policy and value models. But planning with a world model has other advantages as well. We will demonstrate these advantages in two examples below - AlphaGo and Dreamer, where you can have a glimpse of the beauty of model based reinforcement learning.

AlphaGo

The fact that AlphaGo / AlphaGo Zero was built to simulate and plan was exactly why it was able to play Go at superhuman level. Without using simulation and planning at inference time, the raw neural network of AlphaGo Zero had an Elo rating of 3055, which is a top professional level, but still very far from beating human world champions, whose Elo ratings are usually more than 3800.

In the game of Go, the world is very simple - a 19 by 19 board with simple algorithmic rules and two opponents that take turns to place a stone to the board. The state of the world is the positions of the stones and which player is taking the next turn. For AlphaGo, simulation is therefore predicting what the board would like after it places its stone and an opponent places their stone. Since a competent opponent can be simulated by AlphaGo’s own neural network, AlphaGo doesn’t need a separate world model; its world model is just a copy of its neural network with rules applied on top to determine the board state and the immediate reward (i.e. win or lose if it is a terminal state).

Inviting a human Go master to play with and train AlphaGo is expensive and unscalable, but AlphaGo’s world model (you can also call it self-play in this case) allows AlphaGo to do intensive planning effectively to come up with high quality episodes for learning. The planning strategy used by AlphaGo is known as “Monte Carlo Tree Search” (MCTS). AlphaGo¹ maintains a tree of expanded and unexpanded nodes, which initially contains only the current board state. Every time, it selects an unexpanded node with highest potential, and further expands the node with possible children nodes, which becomes available for selection in the next iteration. It then evaluates its value (win rate) and propagates the statistics up the search tree. This process is repeated until time is exhausted and the most visited second level node is selected as the next move. MTCS is very similar to how humans simulate different plays within our brain; the difference is that machines can do it on a much larger scale and in a much more quantitatively precise way.

World models not only provide high quality labels for learning policy and state value estimates; they also provide a different way to solve the credit assignment problem.

A Different Way to Tackle Credit Assignment Problem

As we have discussed earlier in this series of articles, one of the biggest challenges in RL is the credit assignment problem - if an action at state s_t results in a return (accumulated future rewards) of g_t, how much should I assign credit to the current action versus the actions that the agent takes subsequently? In the first three posts of this series, we have discussed REINFORCE, A2C, GAE and PPO. All of these algorithms share the same procedure - they sample episodes under the current policy, and use the sampled episodes to calculate the gradient for updating the policy.

In a model-free reinforcement learning setting, the challenge of credit assignment comes from the fact that the environment is a black box to the learning algorithm; all the agent can do is to take lots of different actions and observe the outcomes to estimate how the environment rewards different behaviors. In a simulated world where the dynamics are governed by a known, differentiable function (the world model), there is a much more robust way to assign credit and learn the policy.

Let’s say in the simulated world all episodes start with the same state s₀ and end after T steps. The simulated world is governed by the world model, which produces the next state s_t = q(s_t-1, a_t-1; w) and immediate reward r_t = r(s_t; w). Given a policy a_t = π(s_t; θ), we can calculate all future T states and rewards:

• a₀ = π(s₀; θ)

• s₁ = q(s₀, a₀; w), r₁ = r(s₁; w), a₁ = π(s₁; θ)

• s₂ = q(s₁, a₁; w), r₂ = r(s₂; w), a₂ = π(s₂; θ)

• …

• s_T = q(s_T-1, a_T-1; w), r_T = r(s_T; w)

Note by repeatedly using the formulas above to expand, every r_t can be expressed as a differentiable function of s₀, θ and w. For example,

\(\begin{align*} r_2 &= r(s_2; w) \\ &= r(q(s_1, a_1; w); w) \\ &= r(q(q(s_0, a_0; w), \pi(s_1; θ); w); w) \\ &= r(q(q(s_0, \pi(s_0; \theta); w), \pi(q(s_0, a_0; w); θ); w); w) \\ &= r(q(q(s_0, \pi(s_0; \theta); w), \pi(q(s_0, \pi(s_0; \theta); w); θ); w); w) \end{align*}\)

The total return, which is the sum of r₁, …, r_T with exponential decay factor λ, can thus be expressed as a differentiable function of s₀, θ and w as well. When s₀ and the world model is fixed, this becomes a differentiable function of θ, and we can use gradient ascent on this giant function to find the locally optimal policy parameter θ; no sampling and estimation is needed!

Of course, this is an idealized scenario. In reality, if T is too large, the world model will likely accumulate too much error to generate a good estimate of return in the real environment. However, world models provide a different way to solve the credit assignment problem, which is utilized by the Dreamer agent discussed below.

Dreamer

Developed by Google DeepMind, Dreamer is an RL agent that learns to achieve goals in the digital environment from pure image input. Dreamer v3 was the first algorithm to collect diamonds in Minecraft from scratch without human data or curricula, which was a significant achievement for AI. We will use Dreamer v1 as an illustrative example in this article for its simpler architecture.

At a high level, the training of Dreamer v1 looks like this:

Initialize an FIFO dataset D with some random seed episodes from the actual environment

While not converged do:

  Repeat C Steps:

    Sample B (observation, action, reward) sequences of length L from D

    Use the sequences to update the world model

    Generate an imagined trajectory of length H for each sampled state

    Use the imagined trajectories to update the agent’s policy

  Sample a new episode from the actual environment and add to D

Dreamer’s world model, which is a recurrent neural network, learns to represent the state of the environment with a vector s_t. Given the previous state s_t-1 and action a_t-1, it predicts the next state and rewards q(s_t-1, a_t-1; w), and r(r_t | s_t; w). One of the objectives to train the world model is how good it can predict the reward from the actual environment. Another objective is to reduce reconstruction error - the difference between the next image from the actual image and the image reconstructed from the next predicted state. There are other objectives which I will not go into the details - interested readers can refer to section 4 of the Dreamer v1 paper.

Figure 2. From Dreamer v1 paper: comparing the actual image and the reconstructed image.From the latent state. The reconstructed images start to deviate from actual environment as more steps are simulated.

Dreamer’s policy model is trained on this latent state to select the action that maximizes future return; it never sees the raw images from the actual environment, hence the name “dreamer”. However, instead of dreaming (planning) till the end, it dreams 15 steps ahead, which gives the policy model the total rewards from the future 15 steps. In order to have an estimate of the full return, Dreamer introduces another value network to estimate the expected return of a state v(s_t) = v(s_t; ɸ). The estimated return of an action can thus be expressed as the sum of the imagined reward of the first 15 episodes, plus the state value of the 15^th imagined state². This estimated return is still a differential function of θ, which you can solve analytically.

Dreamer uses the world model to roll out an imagined trajectory and a policy model to estimate the residual value of the trajectory, which is very similar to AlphaGo’s MCTS, where simulated plays are rolled out before a policy model is involved to estimate the value for the rest of the play. The biggest difference is that MCTS considers many possible trajectories while Dreamer only rolls out one trajectory.

The Biological Inspiration

Neural network, deep learning, attention, chain of thought… Many of the concepts in ML/AI are inspired by biology & human cognitive, so it is not surprising that the concept of internal world model has its deep biological root as well.

It used to be widely believed that the brain passively receives and processes sensory information. That theory has been largely superseded; there is a strong consensus in cognitive science that the brain is an active and dynamic organ that constantly generates its own activity to shape our perception. It predicts what we are going to see next, and it predicts what it feels like when we are reaching out to grab something. These predictions separate expected changes from surprises, allowing the brain to act swiftly while minimizing the amount of effort. From this perspective, we all live in a half-dreaming state.

Our internal world model, like other biological systems, is the product of hundreds of millions of years of evolution, which has made it incredibly energy-efficient and adapted to the physical world. While we can never hope to artificially replicate this vast process, we can draw inspiration from its results. By drawing inspirations and making deliberate tradeoffs based on our own needs, we create technologies that are useful for humanity - inventions that are simultaneously superior and inferior to their natural counterparts.

1. This is actually the description AlphaGo Zero’s MCTS, which is similar (but simpler) than AlphaGo’s.

2. The actually implementation in the paper is more complicated than this but the idea is the same.