Life through the Eyes of a Bayesian
An invitation to think like a Bayesian.
If I ask you what you have learned from science and mathematics that has the most profound impact on you, what would your answer be?
For me, the answer changes over time; but if you asked me in the last couple of years, my answer would likely be Bayes’ theorem. The reason is pretty simple - all other widely applicable theorems that I can think of deal with some object in the external world, be it real or imaginary; Bayes’ theorem however, connects the external world and our mind.
![\bbox[#eeeeee, 5px]{P(A|B)=\frac{P(A)P(B|A)}{P(B)}\propto P(A)P(B|A)} \bbox[#eeeeee, 5px]{P(A|B)=\frac{P(A)P(B|A)}{P(B)}\propto P(A)P(B|A)}](https://substackcdn.com/image/fetch/$s_!6441!,w_1456,c_limit,f_auto,q_auto:good,fl_progressive:steep/https%3A%2F%2Fsubstack-post-media.s3.amazonaws.com%2Fpublic%2Fimages%2F00ab5257-a760-4258-900c-de6654f6df73_627x194.png)
I remember years ago, when I only knew about the frequentist definition of probability, a college introduced me to Bayesian statistics. When he told me that probability reflects your personal belief and I could choose my prior, I panicked - the equation is pretty simple and easy to understand, but the interpretation is “scary”. How should I pick my prior for my hypothesis? Science is supposed to be objective and unquestionably true; if I could pick my own prior, wouldn’t the conclusion become subjective? How can I convince other people if the conclusion is my subjective view?
As I grow and learn, especially after I got to a place where people were counting on me to make decisions, I realize relying on prior to make conclusions and decisions is a natural part of us, and it will be an empowering tool if you deliberately embrace it.
If you struggle to grasp your own prior to make decisions like me, at least there is some good news - prior doesn’t really matter when there is overwhelming evidence. When I say overwhelming evidence, I mean lots of dependent data points that support the argument. This may sound like common sense, but if we derive it mathematically, it will allow more insightful discussions.
Let’s say observation B contains multiple independent data points, B1, B2, …, BN. In order to compare whether A or Ā (the opposite of A) is more likely after observing B, we can check whether P(A|B) / P(Ā|B) is greater than 1. Based on Bayes’ theorem and the fact that all Bi are independent, we have:
Suppose all observed data points supports A more than Ā, namely there exists a ε > 0, such that
, then we have
Because the weight from evidence grows exponentially, it will quickly dominate the posterior odds P(A|B) / P(Ā|B) as independent data points are gathered.
If there is a life lesson to draw from the equation, it would be open-mindedness - always open to admit mistakes or change direction when evidence shows that your previous hypothesis was less favorable.
However, this is just an idealized model. In reality, things are much more complicated.
In my kids’ Chinese literature book, there is a story called Gu Dong Is Coming (which itself is based on an ancient Chinese folk tale). In the story, a rabbit was playing near a lake, when it suddenly heard a loud “Gu Dong” sound. Panicking, the rabbit started to run away, shouting, “Gu Dong is coming!” Seeing and hearing the panicking rabbit, the monkey started to run and shouting “Gu Dong is coming” as well. Later, the fox and the bear joined, and soon, almost all the animals were running out of the jungle, shouting “Gu Doing is coming”, until they were stopped by the tiger. The tiger asked, “What is Gu Dong?” Nobody could answer that question but the tiger traced down the origin of the panic to the rabbit. The rabbit took the animals to the lake. They waited and waited until they heard the “Gu Dong” sound again - it was ripe papayas falling down from the tree.
I like the story because for the tiger, it is a very interesting decision making problem. Going back to the formula from the last section,
let’s say A is the hypothesis that there is something terrible happening, and let Bi be the event that animal i is running in panic and shouting “Gu Dong is coming”. Bi appears a good indicator of something terrible happening to them, so P(A|Bi) / P(Ā|Bi) should be much larger than 1. There are lots of animals running and shouting so N is large, which means the product of P(A|Bi) / P(Ā|Bi) should be astronomical. Regardless how much you disbelieve that a horrible Gu Dong is coming, the only sensible thing to do is to run, run for your life!
And so did other animals. But the tiger’s sanity check revealed a few key pieces of information. First, nobody saw or even knew what Gu Dong was, so P(A|Bi) / P(Ā|Bi) was actually much smaller than it first appeared. Secondly, everyone got the information from a single source - the rabbit - which means there was only one data point instead of N. Lastly, since the source was the rabbit, how much would that apply to the much stronger tiger? From the tiger’s perspective, P(A|Brabbit) / P(Ā|Brabbit) should probably be close to one, and the prior should be the dominating factor of posterior!
The story also highlights a deep philosophical question - how much should one trust what they see or hear? Evidence is subjective as well, and based on our prior, we (rightly) trust some over the other. We trust what we see over what we hear, and we trust what we see because of what we proactively do over what we see passively. What Bayes's theorem tells us then, is how we should weigh different sources of subjective evidence, and how we should weigh our gut against the subjective evidence.
For a long time, humans lived in a condition where information sharing and knowledge acquisition had lots of barriers, and therefore, it was very hard to form strong evidence to prove or disprove a theory about how our world works. However, as humans, we desire explanations to important questions about our life. Lack of evidence was then compensated by strong priors to provide explanations to everything that matters - from life, death, illness, disaster, to fortune and power. Strong priors created strong bonds among people holding the same ones, but it also resulted in stagnation and conflicts among people holding different priors.
Things started to change with the invention of paper and the printing press, which greatly lowered the barrier of information sharing. Fast forward to the 21st century, information has become almost zero cost to produce, transmit and consume. Today, a vast majority of us live in an evidence heavy world. Everything is quantified as numbers which allows you to consume without understanding its real meaning. Things that happened thousands of miles away are delivered to you in images, videos and live streams that make it feel intimate to you. An opinion from one source is amplified by social media as an opinion from many. It is fair to say that the story of Gu Dong Is Coming is happening every day everywhere.
To make educated decisions in this evidence-heavy world, we need to learn from the tiger. We should check our prior, and make sure we are not carried away by how dramatic the evidence looks like. We should understand the true strength of evidence and how much it relates to our current context, and make conclusions and decisions based on the combination of prior and evidence.
Even more importantly, your priors will be constantly improved through the process of making those informed decisions and observing their outcome. The priors you build over time are unique to you; they are based on your value, your strength, your domain and your circumstances, which is irreplaceable by the ever-changing, context-unaware evidence.


![\bbox[#EEEEEE, 8px]{
\frac{P(A|B)}{P(\overline{A}|B)}=\frac{P(A)P(B|A)/P(B)}{P(\overline{A})P(B|\overline{A})/P(B)}=\frac{P(A)}{P(\overline{A})}\cdot\frac{P(B|A)}{P(B|\overline{A})}=\frac{P(A)}{P(\overline{A})}\prod_{i=1}^N\frac{P(B_i|A)}{P(B_i|\overline{A})}} \bbox[#EEEEEE, 8px]{
\frac{P(A|B)}{P(\overline{A}|B)}=\frac{P(A)P(B|A)/P(B)}{P(\overline{A})P(B|\overline{A})/P(B)}=\frac{P(A)}{P(\overline{A})}\cdot\frac{P(B|A)}{P(B|\overline{A})}=\frac{P(A)}{P(\overline{A})}\prod_{i=1}^N\frac{P(B_i|A)}{P(B_i|\overline{A})}}](https://substackcdn.com/image/fetch/$s_!tIMB!,w_1456,c_limit,f_auto,q_auto:good,fl_progressive:steep/https%3A%2F%2Fsubstack-post-media.s3.amazonaws.com%2Fpublic%2Fimages%2F48c59334-90c6-48cc-9863-f32f7e5b3e82_818x96.png)
![\bbox[#EEEEEE, 8px]{
\frac{P(B_i|A)}{P(B_i|\overline{A})} > 1+\epsilon \text{, for any }i} \bbox[#EEEEEE, 8px]{
\frac{P(B_i|A)}{P(B_i|\overline{A})} > 1+\epsilon \text{, for any }i}](https://substackcdn.com/image/fetch/$s_!BT0i!,w_1456,c_limit,f_auto,q_auto:good,fl_progressive:steep/https%3A%2F%2Fsubstack-post-media.s3.amazonaws.com%2Fpublic%2Fimages%2F924f7656-43a6-4f89-be5c-4c4b10cd6952_311x89.png)
![\bbox[#EEEEEE, 8px]{
\frac{P(A|B)}{P(\overline{A}|B)}=\frac{P(A)}{P(\overline{A})}\prod_{i=1}^N\frac{P(B_i|A)}{P(B_i|\overline{A})}\ge\frac{P(A)}{P(\overline{A})}\cdot(1+\epsilon)^N} \bbox[#EEEEEE, 8px]{
\frac{P(A|B)}{P(\overline{A}|B)}=\frac{P(A)}{P(\overline{A})}\prod_{i=1}^N\frac{P(B_i|A)}{P(B_i|\overline{A})}\ge\frac{P(A)}{P(\overline{A})}\cdot(1+\epsilon)^N}](https://substackcdn.com/image/fetch/$s_!Jg5j!,w_1456,c_limit,f_auto,q_auto:good,fl_progressive:steep/https%3A%2F%2Fsubstack-post-media.s3.amazonaws.com%2Fpublic%2Fimages%2Fa3a664c3-9db5-4750-8c86-a51abef49c15_564x96.png)
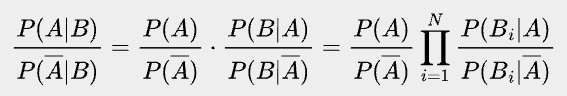

The Story of Gu Dong exists in all culture...I realized in my childhood I also a read a similar story in odia language about a jackal running claiming the earth is going to explode after hearing the sound of wood apple falling and there also at the end the tiger solved it..The idea of bayes theorem is fascinating and so true...